Sun, 03 Sep 2006

Ocaml : Variant Types and Pattern Matching.

At last month's SLUG meeting, Mark Greenaway asked if anybody knew of any good Computer Algebra Systems (CAS) available under Linux. I spoke up and told him that I looked around for the same thing some time ago, couldn't find anything that I liked so I ended up writing something that fit my particular needs from scratch.

Later that night I was talking to Robert Collins and Andrew Cowie about stretch languages; languages that differ radically from the languages a programmer already knows so that learning the new language teaches them new programming concepts and paradigms.

For me, my last stretch language was Ocaml which I started using around mid 2004. I discovered Ocaml when I went looking for a language to implement my Computer Algebra System (CAS) in. I did do a trial implementation in C, but that was simply too much of a pain in the neck. I also knew that C++ was not a sufficiently big step away from C to be useful for this project. My other main language at the time was Python, but I knew Python's dynamic typing would make my life difficult.

It was at about this time that I asked my friend André Pang to suggest a language. André had recently given a talk at SLUG titled "Beyond C, C++, Python and Perl" and seemed to know about a whole bunch of different languages. I told him that I was looking for something that was strongly typed, statically typed, had garbage collection for memory management and had Object Oriented (OO) features.

One of André's suggestions was Java which I was already familiar with. However, I disliked the fact that Java does not allow one to write code outside of a class and Java was also a little too verbose for my tastes. He also tried to push Haskell, but Haskell doesn't have traditional OO features. In retrospect this wouldn't have been a problem, but at the time I rejected Haskell for this reason. However, his final suggestion was Ocaml which seemed to fit all of my requirements. While investigating Ocaml I found a small example on the Ocaml Tutorial that implemented a bare bones CAS.

The two things that makes Ocaml really great for CAS are variant types and pattern matching on these variants. I'll look at these separately.

Variant Types in Ocaml.

Ocaml's variant types are a little like a type safe, bullet proof version of unions in C and C++. In Ocaml one defines a variant type like this: 

type expr_t =
    |  Var of string
    |  Plus of expr_t * expr_t
    |  Times of expr_t * expr_t
    |  Divide of expr_t * expr_t

So, here we have a type named expr_t (a mathematical expression) that can hold one of four things:

All of the sub expressions are of the same type, expr_t, which makes this a recursive type. Using this recursive variant type, an expression like "x * (y + z)" can be build like this: 


let expr = Times (Var "x", Plus (Var "y", Var "z")) ;;

which results in a tree structure with each operator and our variables x, y and z being held in a node of type expr_t and represented by a circle in this diagram:

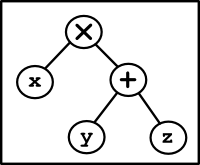
expression tree

with the variable expr being the Times node at the top of the diagram.

The really nice thing about variants is that each instance knows which variant it is. That means that its not possible (by mistake or on purpose) to access a node of one variant as another variant. The Ocaml compiler simply won't let that happen.

Compare this to a C version using unions where the programmer has be make sure he/she accesses each instance correctly, or the acres of code required to do the same thing with objects in C++ or Java.

Pattern Matching on Variants.

So once we can construct a mathematical expression we would also want to print it out. Thats where Ocaml's pattern matching comes in. Here's a function to convert any expression tree into a string representation that can be printed. 

let rec str_of_expr expr =
    match expr with
        |   Var v -> v
        |   Plus (a, b) ->
                "(" ^ (str_of_expr a) ^ "+" ^ (str_of_expr b) ^ ")"
        |   Times (a, b) ->
                (str_of_expr a) ^ "*" ^ (str_of_expr b)
        |   Divide (a, b) ->
                (str_of_expr a) ^ " / " ^ (str_of_expr b)

The function is called str_of_expr and the "rec" just before the function name means that the function is recursive. The function takes a single parameter of type expr_t and returns a string.

The "match expr with" on the next line is a bit like a switch statement in C, C++, Java and other languages. On the lines following the match there are four options, one for each of the variants of the expr_t type. So for instance, if the expr is a Var variant the function just returns the string that is held by Var and if its a Plus node with two sub expressions, a and b, then the function is called on each of the sub expressions and a string is built using Ocaml's string concatenation operator "^".

The above usage of pattern matching is pretty simple and can done almost as easily in other languages. So lets look at something a little more complicated.

More Advanced Pattern Matching.

One of the many things one might want to do in a CAS is applying mathematical transforms on an expression. For instance, we might want to be able to expand out our expressions above "x * (y + z)" to give "(x * y + x * z)". Fortunately, using Ocaml's advanced pattern matching this is really easy. Here's an example: 

let rec simplify expr =
    match expr with
        |   Times (a, Plus (b, c)) ->
                Plus (simplify (Times (a, b)), simplify (Times (a, c)))
        |   Divide (Divide (a, b), Divide (c, d)) ->
                Divide (simplify (Times (a, d)), simplify (Times (b, c)))
        |   anything -> anything (* Comment : default case *)

The function simplify has two transformations and a default case which does nothing. Again, the function is recursive, but the first two match cases match on much more complex expression trees. In fact, the first match case will exactly match our expression and generate the expression we're after, "(x * y + x * z)".

Obviously, to make a real Computer Algebra System requires quite a bit more than what I have here. However, as you can see, Ocaml's variant types and pattern matching are a perfect fit for the problems a programmer writing a CAS would face. In fact, few other languages, with the possible exception of Haskell, would have fit this problem as well.

Posted at: 12:53 | Category: CodeHacking/Ocaml | Permalink